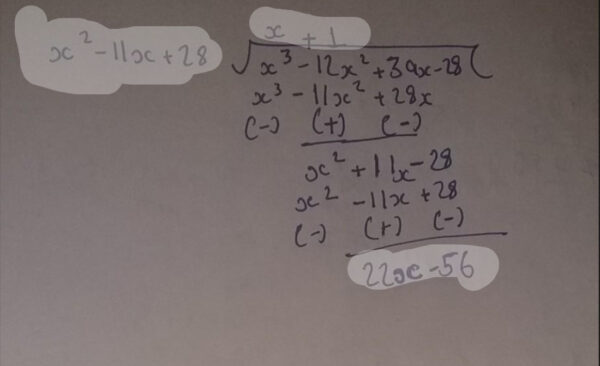
x²-11x+28=0 solved: Welcome to an exploration of quadratic equations, an critical a part of algebra and mathematics. In this text, we can delve into the world of quadratic equations, with a particular consciousness at the equation x²-11x 28=0. Throughout this comprehensive dialogue, we are able to uncover the overall concept of quadratic equations, discover a variety of methods to solve them, and behavior a deep dive into a specific case observe to apprehend the realistic programs of these equations.
Understanding Quadratic Equations x²-11x 28=0
What is a Quadratic Equation?
To embark in this journey, we have to first draw close the essence of a quadratic equation. A quadratic equation is a second-diploma polynomial equation, characterised with the aid of the squared variable. The most fundamental shape of a quadratic equation is expressed as: ax^2 bx c = 0
In this equation, ‘a,’ ‘b,’ and ‘c’ represent coefficients, at the same time as ‘x’ stands for the variable. The equation x²-11x 28=0 precisely aligns with this wellknown form.
General Form of a Quadratic Equation
Understanding the overall form of a quadratic equation is pivotal because it underpins the muse of those equations. By spotting this structure, we are able to effortlessly become aware of the coefficients ‘a,’ ‘b,’ and ‘c.’ For our specific equation, ‘a’ is 1, ‘b’ is -eleven, and ‘c’ is 28.
Solving Quadratic Equation x²-11x 28=0
Quadratic equations are a realm of mathematical issues that can be tackled using diverse techniques. Let’s discover two prominent strategies:
Factoring
Factoring is a method hired to resolve quadratic equations that may be be effortlessly damaged down. However, for equations as complex as x²-11x 28=0, factoring won’t be the maximum straightforward method.
Quadratic Formula
The quadratic method emerges as a versatile and universally relevant technique to fixing quadratic equations. This formula, regularly known as upon, is:
x = (-b ± √(b^2 – 4ac)) / 2a
With this method, we reap the roots of the equation, representing the values of ‘x’ that render the equation identical to zero.
X^2-11x 28=zero: A Case Study
Intriguingly, we now flip our interest to the particular equation x2-11x 28=zero. Our exploration will contain a step-through-step evaluation using the quadratic formulation.
Step 1: Identifying the Coefficients
To initiate this journey, we have to first perceive the coefficients. In the equation to hand, ‘a’ is 1, ‘b’ is -11, and ‘c’ is 28.
Step 2: Applying the Quadratic Formula
With the coefficients now in our hold close, we are able to proceed to use the quadratic formula. The equation takes form as follows:
x = (-(-11) ± √((-eleven)^2 – four * 1 * 28)) / (2 * 1)
In the pursuit of an answer, we simplify the equation, leading to:
x = (11 ± √(121 – 112)) / 2
x = (eleven ± √nine) / 2
Step 3: Finding the Roots
As the equation begins to crystallize, we uncover two ability solutions:
x = (eleven 3) / 2 = 7
x = (11 – three) / 2 = 4
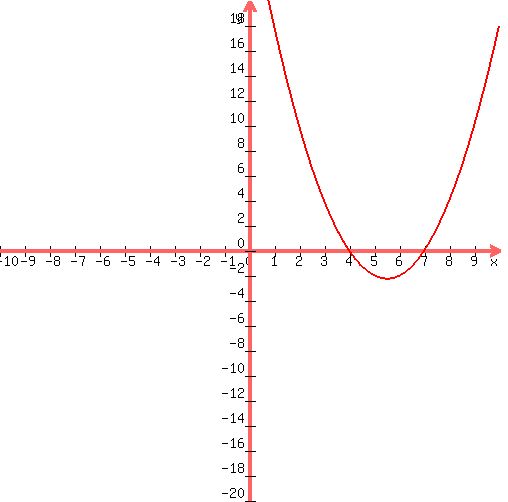
Thus, the roots of the equation x2-11x 28=0 are found out as x = 7 and x = 4.
Graphical Representation of Quadratic Equations
In the world of quadratic equations, the graphical depiction regularly takes the shape of a parabola. This U-fashioned curve offers critical insights into the behavior of these equations, with the vertex being a critical factor, signifying either the minimum or most of the parabola.
Applications of Quadratic Equations
The practicality of quadratic equations transcends idea, locating packages in diverse domain names which include physics, engineering, and economics. In those real-international eventualities, quadratic equations serve as effective tools to version and solve problems with precision.
Conclusion
To sum up, delving into the world of quadratic equations has been a captivating adventure. In this text, we have unraveled the essential principles surrounding quadratic equations, unraveled the method of fixing them the usage of the quadratic formula, and witnessed the realistic implications via a specific case observe, specifically x2-11x 28=zero. Furthermore, we’ve got explored the visual representation of quadratic equations thru parabolic graphs and highlighted their real-international relevance in various applications.
